Tsunami Modeling
Three basic equations underlie tsunami models. They are an equation of continuity and two horizontal equations of motion. The equation of continuity looks like this:
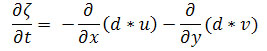
Where ζ = sea level, u is the east-west component of velocity (positive is east), v is the north-south component of velocity (positive is north), x is distance east and y is distance north, and the non-derivative d is depth.
The equation says something like “the change in sea level over time is equal to the amount of water moving in or out in the east-west direction plus the amount of water moving in or out in the north-south direction.” This equation accounts for the fact water is virtually incompressible, and says that if water rushes in from four sides into a rectangular prism, it has to equal the water that rises up from the top of it. Water in equals water out.
Equations of motion are more complicated versions of the familiar equation force equals mass times acceleration. The equations of motion, in their simplest form, are
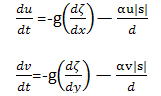
Where u is again the east-west velocity, v is the north-south velocity, the non-derivative d is depth, g is gravity, ζ is sea level, s is the absolute value of the wave’s speed, and α is a dimensionless friction constant. s is defined as the √u2+v2
The second term on the right side of both equations relates to friction. The shallower the ocean (d), the more friction the tsunami experiences. The d-zeta (ζ)term is the slope of the sea level, which says that if the ocean is not flat, a current will form to try to minimize the slope and return it to zero.
These are simplified forms of the equations. Versions that are more fully written out include a term to account for the Coriolis force, or the apparent turn of moving objects due to the rotation of the Earth, non-linear convection terms that account for transport of momentum by wave motion, and the spherical terms, which account for the convergence of lines of longitude at the poles.