Print Version
Propagation
Propagation
Though it's common to think of waves as moving water, in deep water, waves are more flowing energy than moving mass. Think of whipping a rope attached to a wall up and down—though waves travel through it, the rope itself has no net horizontal movement.

Likewise, birds floating at sea stay put as waves travel beneath them.
Wave Properties
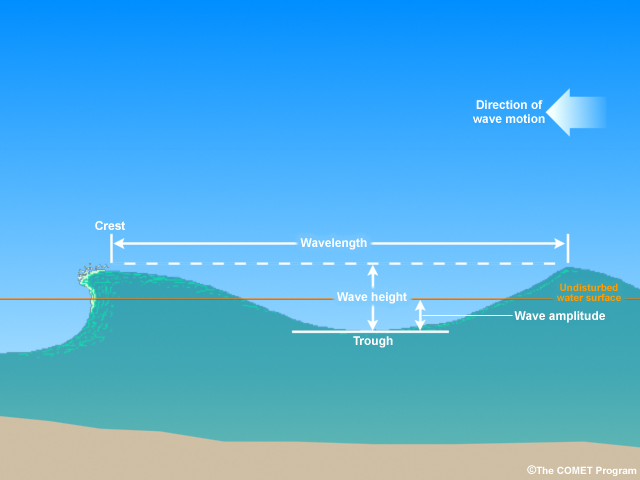
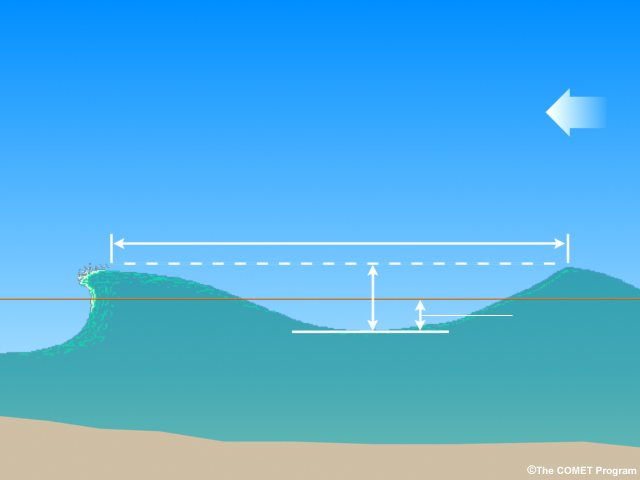
Physicists have described many basic properties of waves. The most basic parts include crests, or high points, and troughs, or depressions. The distance between two successive crests or troughs is called the wavelength, or L. Imagine a wave passing a pier. Marking the difference on the pier between a successive crest and trough would give the wave height, or H. Wave amplitude is the elevation of the wave above or below ambient sea level, and is 1/2 H.
Now imagine starting a stopwatch when a crest passes and stopping it when the next crest arrives. That time is the period, or T. The inverse (1/T) of the period is the frequency, f, or number of wavelengths that pass a fixed point per unit time. These terms are related by the equation Speed(S) = L/T=Lf.
Though all waves possess these basic properties, different wave types display unique patterns of properties.
Deep Water Waves
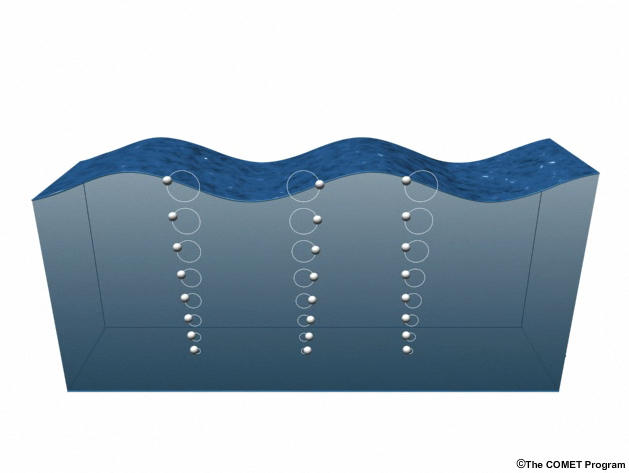
The wind waves familiar to travelers at sea are deep-water waves, so-called because the distance to the ocean bottom is greater (usually far greater) than the wavelength. In this illustration, you can see how wavelength and particle motion relate to depth in deep water waves.
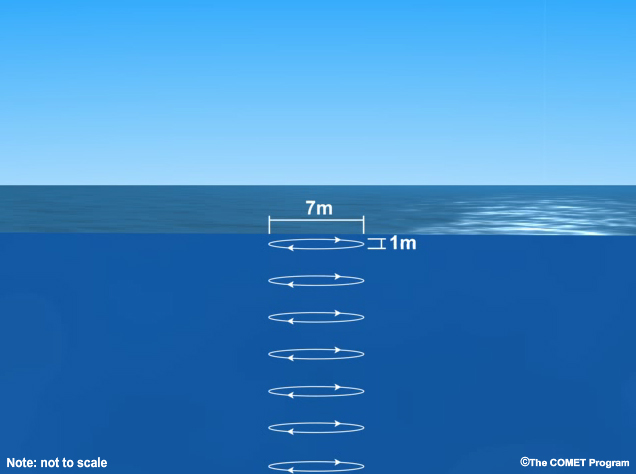
Wind waves have heights at sea proportional to their energy; waves with the most energy are visible as large swell. Water molecules affected by passing deep-water wind waves have circular or slightly elliptical orbits that gradually decrease in diameter with depth. These orbital motions cease at a depth equal to ½ the wavelength. Even during a fierce storm the water is placid below 150 m (500 ft). The bottom of the ocean is completely unaffected by wind-generated waves.
Shallow Water Waves
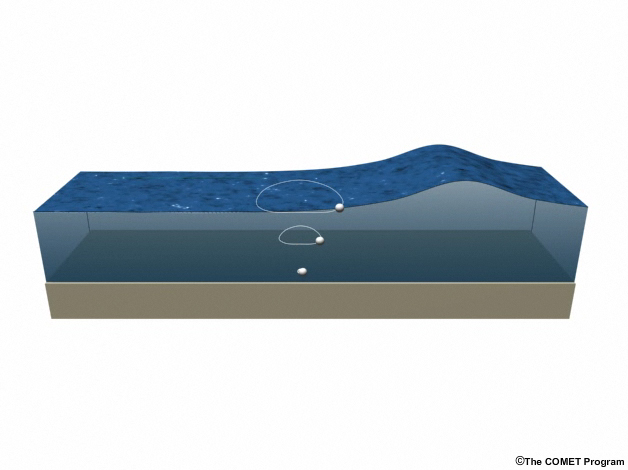
As deep-water waves approach shore, they start to “feel bottom” as the deepest orbits begin to interact with the seafloor. The waves steepen and heighten. Once the depth is less than about one-twentieth of their wavelength, they become shallow-water waves.
In these waves, water particle motion becomes a long flattened ellipse or a horizontal oscillation. While wave speed is slowing down, particle speed accelerates as energy moves from one form to the other. In other words, shallow water waves increasingly become moving water, and not just moving energy, and particle speed becomes comparable to the wave speed.
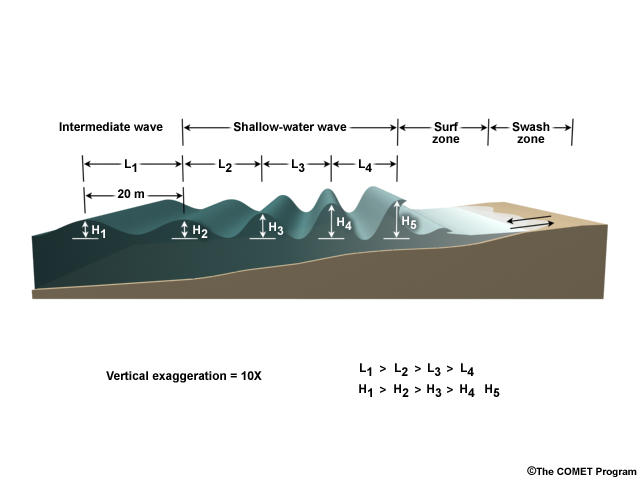
When waves begin to interact with the seabed in shallower water, they slow down, wavelength decreases, and wave height increases.

Eventually, for wind-waves, the steepness becomes too great and they "break," creating the classic curl sought by surfers.
Wave Properties Summary Questions
Question 2
The number of wavelengths that pass a fixed point per unit of time is the frequency. The inverse, or amount of time that passes between successive wave crests, is the period. (Choose the best answer.)
The correct answer is True.
Question 3
(Use the selection box to choose the answer that best completes the statement.)
Deep water wave height is directly proportional to the wave's energy.
Question 4
(Use the selection box to choose the answer that best completes the statement.)
Shallow water waves have wavelengths that are much greater than the depth.
Question 5
(Use the selection box to choose the answer that best completes the statement.)
When shallow-water waves approach shore, wave speed slows, while particle motion accelerates, and wave height increases.
Wind and Tsunami Waves at Sea

At sea, deep-water wind waves travel slowly yet produce relatively high crests, as anyone who has experienced seasickness can attest. Their wavelengths are usually in the dozens or hundreds of meters, with 5-15 second periods and speeds of 1-10 m/s (3.6-36 km/hr, or 3.3–33 ft/s) for waves made by winds of 40 km/h (25 mi/hr) or less. Wind waves are commonly 5-10 m (16-33 ft) high during strong gales, travel 15-20 m/s (49-66 ft/s) and reach 25 m (75 ft) high in hurricane force winds. Wind waves over 30 m (100 ft) tall are not unknown, but this still pales in comparison to the depth of the ocean.
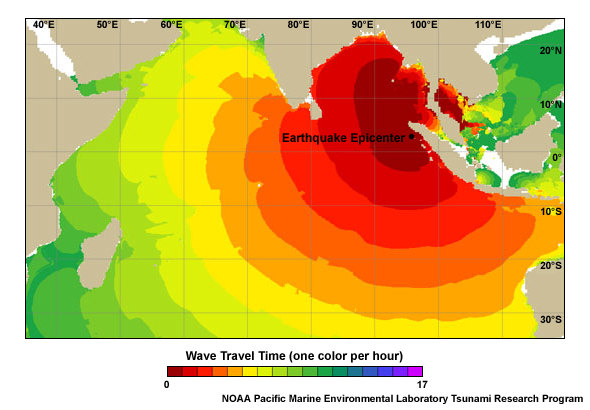
Tsunami waves, on the other hand, have long periods and wavelengths, low amplitudes, and very high speeds. Their velocity approaches those of commercial jets: around 800 km/hr (500 mi/hr), which means they can cover incredible distances in short times. Their wavelengths can be up to 650 km(400 mi) long, while typical periods are 10 minutes to one hour. Yet a large tsunami in open ocean may be only a half a meter (1.6 ft) high. A ship at sea is unlikely to notice anything unusual if a tsunami passes underneath it.
Tsunami Properties
What do you think? Which type of waves are tsunamis?(Choose the best answer.)
The correct answer is B.
Believe it or not, tsunamis are shallow water waves. Water motion associated with the passage of the wave reaches the seabed even in deep water because the entire water column has been forced up over a large area. This makes tsunami wavelengths much longer than the depth of the ocean. The wavelength is roughly equal to the earthquake’s rupture width, which correlates to the width of uplift. As we saw, shallow-water waves form when the distance to the ocean bottom is generally less than one-twentieth of their wavelength. Tsunamis can have wavelengths up to 500 km (300 mi) long—but the ocean bottom averages only a few kilometers deep, making them shallow-water waves from the start.
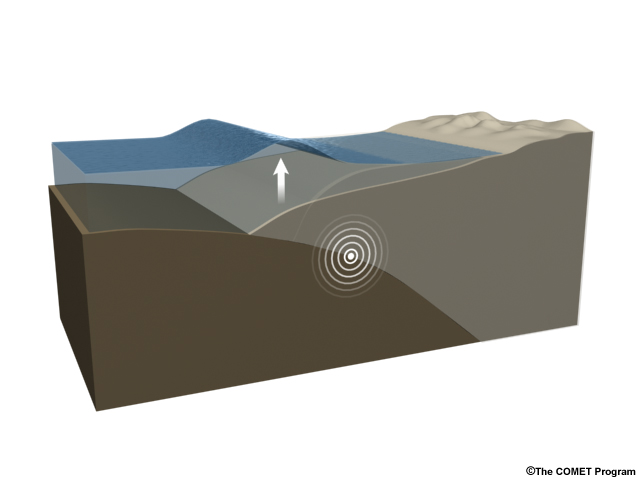
The wavelength of a tsunami is set by the width of sea floor deformation since the initial deformation of the sea surface copies the rupture-induced deformation below. Because one part of the ocean floor generally moves up and another down, this represents the horizontal distance from the crest to the trough of a wave, which is ½ the wavelength. The wavelength determines the period of the wave through the relationship period = wavelength divided by wave speed. For shallow water waves, the wave speed depends on depth according to the formula Speed(v)=√gd, where g is the acceleration of gravity and d is the depth. Thus the width of the deformation and the depth of the water are the key factors in determining tsunami period. Notice wave speed is independent of wavelength or height, depending only on gravity and depth. This is not the case for deep water waves, where wave speed depends on gravity and wavelength. Wavelength replaces depth as the controlling variable for speed.
As mentioned in the Initiation section, the initial wave height of a tsunami is also set by the amount of uplift or dropdown on the seafloor. Because water isn’t very compressible, it’s a close relationship. One meter of uplift on the seafloor will typically yield about one meter of wave height above the rupture.
Tsunami Particle Movement
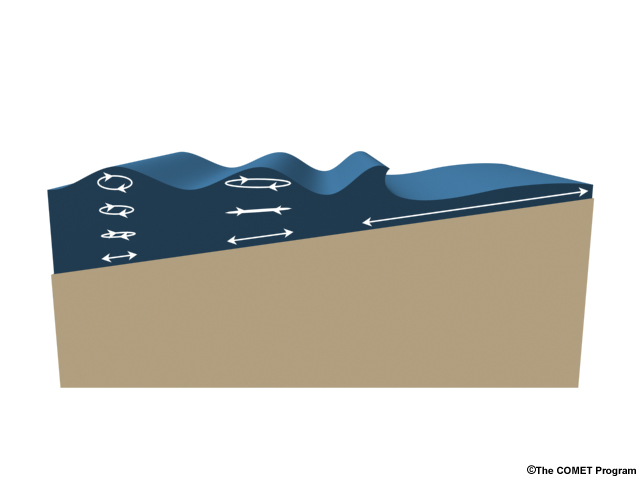
As shallow water waves, tsunami wave speed is inversely related to particle speed. In deep water when waves are traveling fast, each individual particle moves only a few meters horizontally at most. In shallow water, as waves slow down, particles move much farther and the tsunami becomes a movement of water en masse.
You might think of this in terms of energy absorbed per water molecule. In the deep ocean, there are many water molecules between the seafloor and the surface to transmit the energy of a passing wave, so each individual molecule doesn’t move far. This changes at shore, where the energy is concentrated vertically and horizontally. In very shallow water, there are many fewer water molecules between the surface and the bottom. Even as the wave slows down, individual water molecules speed up and run far up the shore before the wave’s energy is spent.
DART buoy observations for a real tsunami

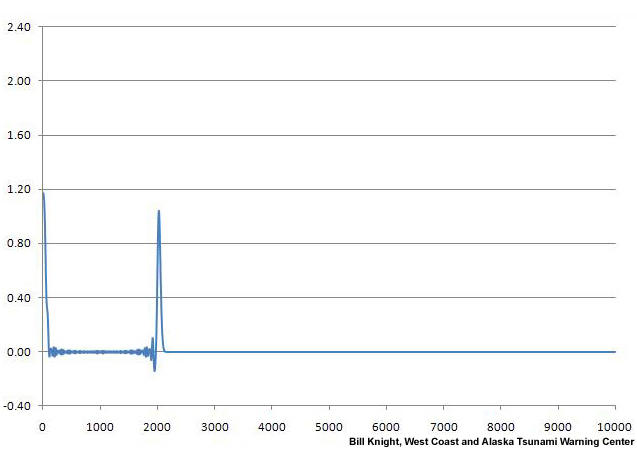
DART buoys deployed by NOAA measure tsunamis at sea. These buoys measure passing tsunamis by sensing pressure changes at the bottom of the ocean.
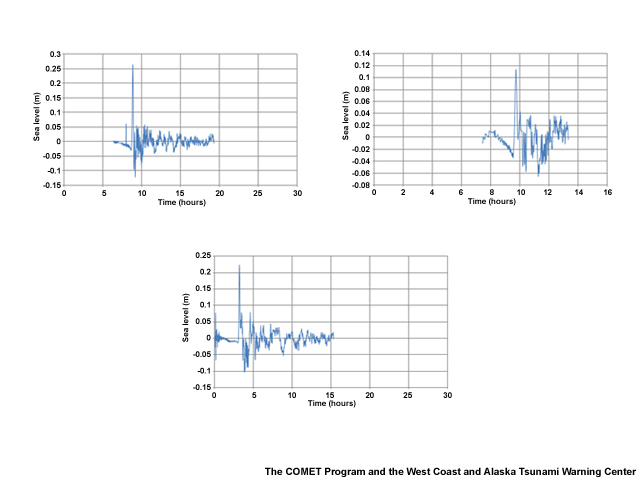
Here are some DART buoy data for the 2010 Chilean tsunami. In the bottom graph, you can see the seismic surface wave arrive before the big initial spike of the tsunami.
Summary Questions
Question 1
Deep Water Waves vs. Tsunamis (Use the selection box to choose the answer that best completes the statement.)
| Characteristics | Deepwater Wind Waves | Tsunami Waves |
| Period | Short | Long |
| Part of Water Column Affected | Top | Entire |
| Orbital Size | Shrinks with Depth | Remains the same with Depth |
| Amplitudes at Sea | Low – High | Low |
| Wavelength | Short | Long |
Question 2
Why are tsunamis considered to be shallow-water waves? (Choose the best answer.)
The correct answer is A. Like wind waves approaching shore, tsunamis are shallow-water waves because their hundreds-of-kilometer long wavelengths are much greater than the ocean's depth.
Question 3
Tsunami waves cause water particle movement all the way to the bottom of the ocean. (Choose the best answer.)
The correct answer is True.
Question 4
(Use the selection box to choose the answer that best completes the statement.)
As tsunamis approach shore, their waves slow down while the water molecules affected by their passing move faster and travel longer distances. Eventually, the wave slows from up to 800 km/hr to 50km/hr (500 mi/hr to 30 mi/hr), but the moving particles become a current running far up the shore.
Tsunami Modeling

Before or during a tsunami, scientists can use seismic data, deep ocean and coastal sea level data, bathymetric data, and tsunami models to help them predict which coasts are most in danger. Like weather forecasters, they run these data through models that use different numerical techniques to solve similar tsunami propagation equations. The solutions to these equations forecast wave height. They can also look at historical records of nearby earthquakes and compare those to the event at hand. This is particularly true in the Pacific Ocean, where good data have been kept ocean-wide for 100 years, and for many centuries before that in Japan.
Tsunami forecast models use an initial condition and boundary conditions to drive the model calculations. The initial condition is the initial sea level perturbation. Boundary conditions are ocean bathymetry and coastal elevation. The initial sea level perturbation is derived from earthquake source parameters including rupture length, width, depth, strike, dip, slip, and moment. The bathymetric/elevation configuration accounts for the shape of the sea floor. Tsunami modeling also accounts for minor effects like friction and the Coriolis Effect.
Given the sea surface perturbation and bathymetric/elevation configuration, tsunami forecast models solve three equations for three unknowns at discrete time steps. Since tsunamis are shallow water waves, assumptions are made which simplify the problem. Vertical particle velocity is considered to be zero, so only the two horizontal equations of motion must be solved in conjunction with the equation of continuity. Forecast model output includes forecast amplitudes and currents, tsunami time series models of projected amplitude at select locations, travel time, inundation extent, energy maps, and other possible results. As with all environmental models, solutions are not exact. Click for more information on tsunami modeling.
Energy directivity
When tsunamis propagate, they don’t do so evenly like the ripples ringing a pebble tossed into a pond. For one, the ocean is a much bigger place.
Over the distances tsunamis travel, the bottom is uneven and the ocean is filled with obstacles that can scatter, steer, disrupt, speed, or slow waves.
For another, tsunami triggers aren’t rounded like pebbles. They’re often unevenly shaped or oblong, since fault ruptures can be hundreds of kilometers long.
When tsunamis emanate from long ruptures, most of the energy is directed perpendicular to the fault. As a result, the waves often seem “beamed” in one direction as might happen if a log fell into water, particularly if the tsunami wavelength produced by a given earthquake is less than the rupture length.
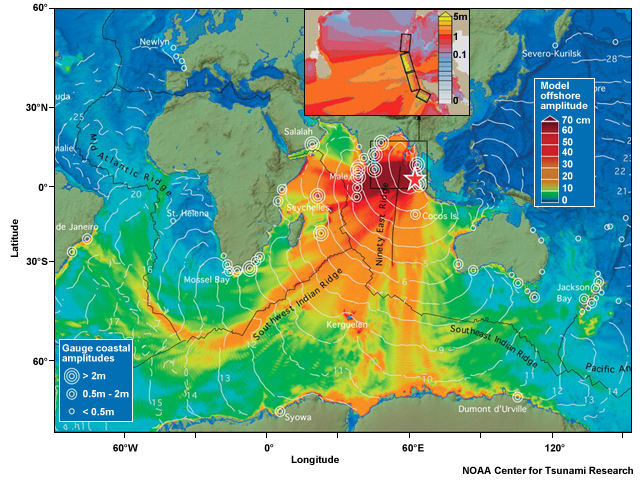
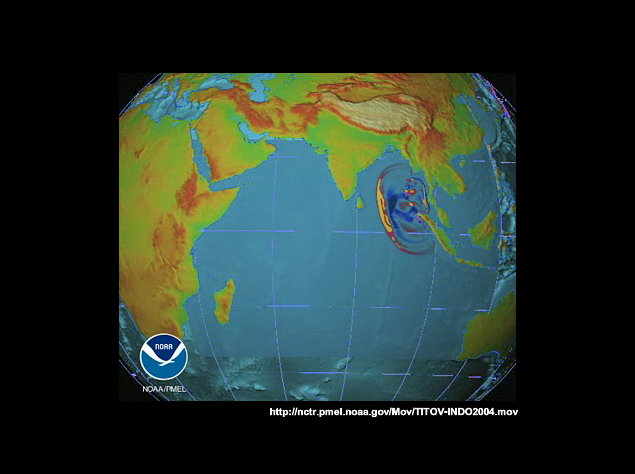
In 2004, India and Sri Lanka felt the full strength of the tsunami because they were perpendicular to the rupture in the east Indian Ocean. The southeastern Indian Ocean, on the other hand, received only weak waves because it was in a “shadow zone.”
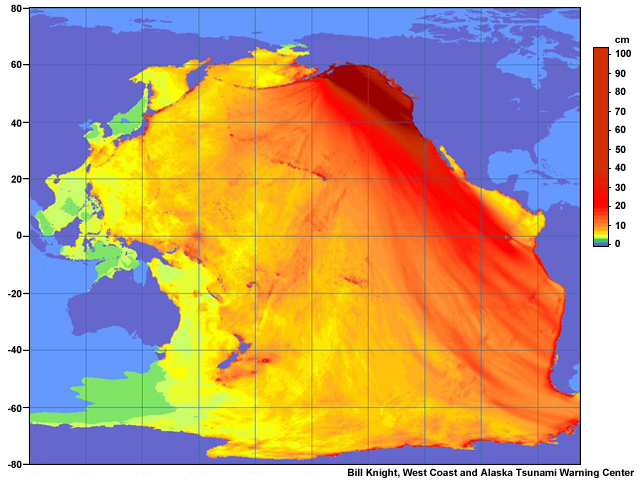
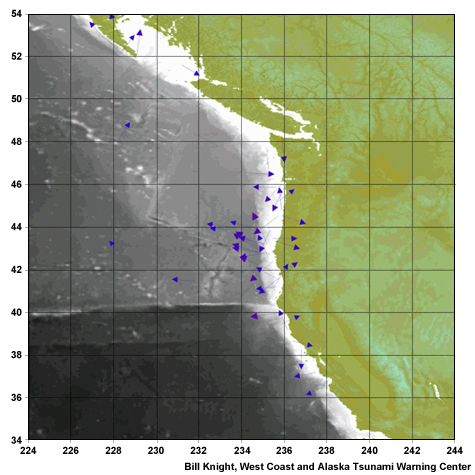
The Alaska earthquake of 1964 “beamed” its waves southeast toward Washington, Oregon, and Northern California.
Reflection
Just like light, tsunamis can reflect off objects, chiefly coastal features. In this series of animations, you can see what happens to ideal waves when they strike a cliff.
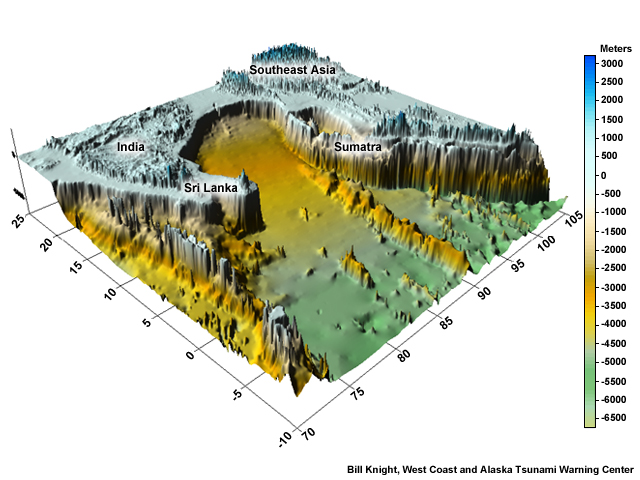
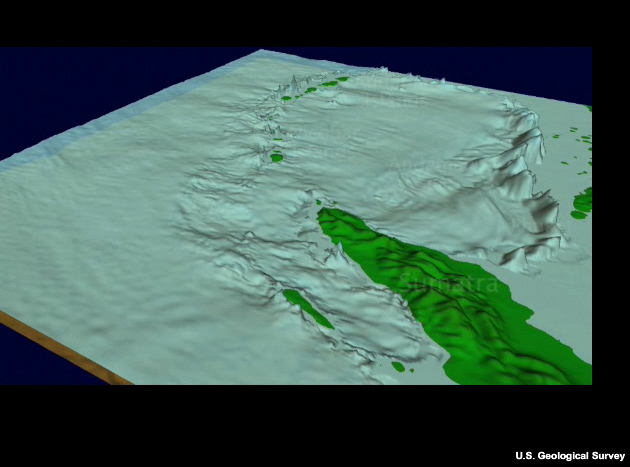
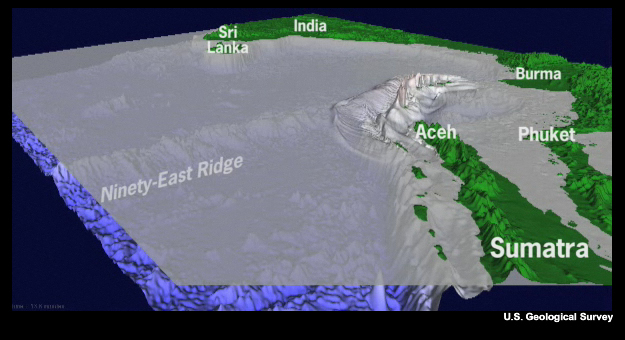
Here is an image of the rise from the Indian Ocean bottom up to the Maldives and Sri Lanka. The steep surface makes an excellent reflector, as you can see in this movie.
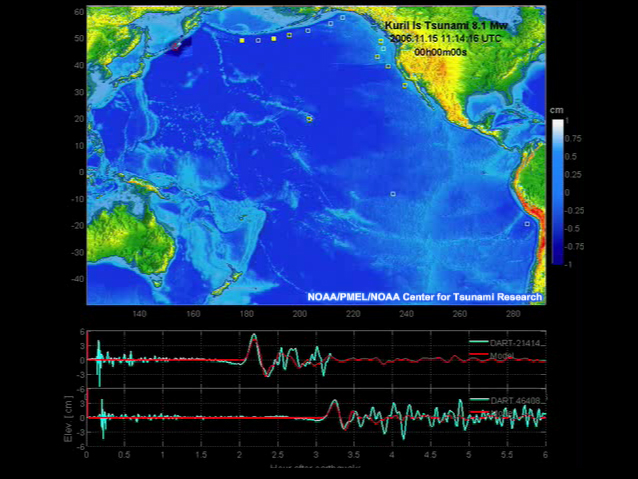
Reflections can create complex and unpredictable wave patterns. In this movie of the 2006 Kuril Island tsunami, you can see how it reflects off the Emperor seamounts and the Hawaiian Ridge, generating complex wave patterns elsewhere.
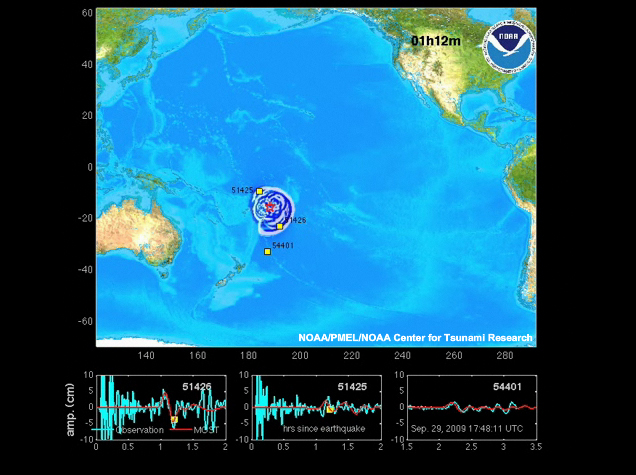
Here is another example—the 2009 Samoan Tsunami. Notice the many reflections, particularly off the coast of California.
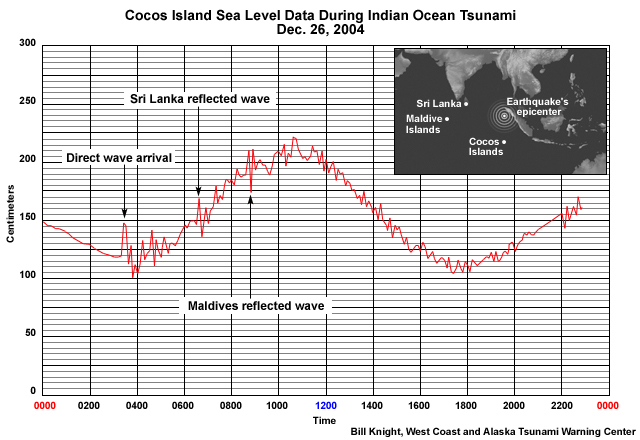
In this marigram of the 2004 Indian Ocean tsunami, you can see waves reflected from Sri Lanka and the Maldives islands at the Cocos Islands in the East Indian Ocean.
Refraction
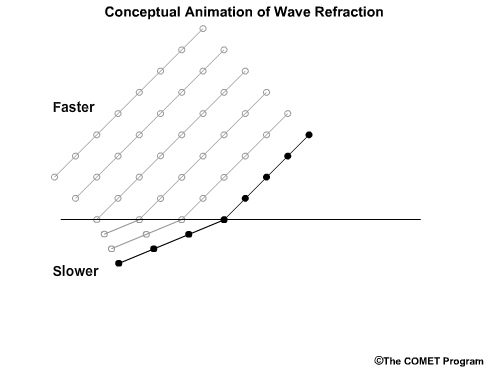
Refraction is the change in the direction of wave movement due to a change in wave speed. These changes in wave speed happen because waves slow down in shallow water. When one part of a wave is in shallower water than another part, the wave bends.
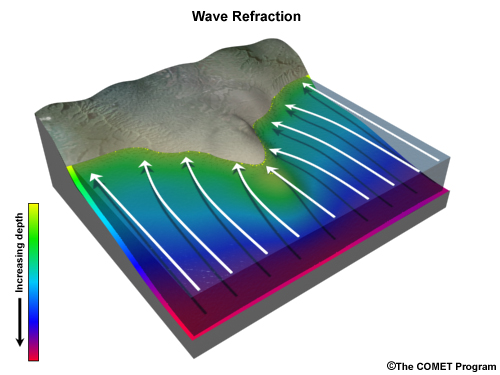
For example, in this illustration of a wave passing by a spit of land as it nears the coast, you can see that the wave turns toward the peninsula.

Here is a real refraction of wind waves off Waikiki Beach in 1946.

Refraction can create some very interesting effects—like channeling. In the Indian Ocean tsunami, you can see how oceanic ridges seemed to channel tsunami waves down their length. This is a refraction effect. At an oceanic ridge, the speed is lowest along the ridge axis since the ocean is shallowest there. Hence the ridges seem to funnel tsunami waves along them.
In this example, you can see how the 2006 Kuril Island tsunami was guided toward shore by the Mendocino Fracture Zone off the coast of northern California. Note the two large pulses of energy. The first is the direct wave, and the second is from an interaction with a large seamount in the Central Pacific.
Convergence
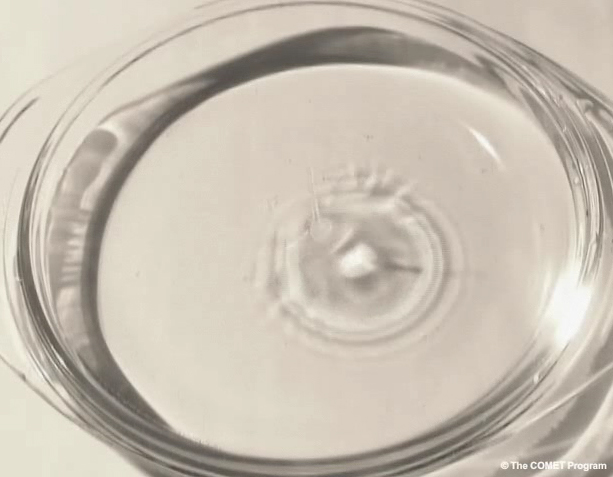
When a drop falls in water, its waves spread out evenly in concentric circles. As they travel, their amplitudes drop as their energy is spread through a larger surface area in accord with the law of conservation of energy.
But now imagine wrapping the plate around a spherical object like Earth. If a drop fell on the water at its north pole, the waves would spread outward and lose height until they reached the equator. But as the waves continued on toward the South Pole, they would begin converging. As a result, the waves would again grow taller.
Similarly, a drop released just above a water-filled pie plate (as shown previously) will produce an expanding wave front that will diminish in amplitude as it travels from the center. After reflection from the rim, the wave front will converge at the center and produce a high-amplitude spike.
Scientists have seen this effect with tsunamis. The 1960 Chilean tsunami occurred in the far southeast section of the Pacific Ocean. Japan, almost halfway around the globe, experienced large waves due in part to convergence.
Coriolis Effect
As with storm systems traveling through the atmosphere, tsunamis are subject to the apparent Coriolis force that comes with traveling on a rotating, round planet. The Coriolis force makes things traveling a straight path seem to veer right in the northern hemisphere and left in the southern hemisphere. This effect can have a minor influence in forecasting long-distance tsunamis, and tsunami models account for it.
Dispersion
Earthquakes and submarine landslides generate waves comprised of many different wavelengths. Though these waves mostly travel the same speed, waves of longer wavelength travel a bit faster than those of shorter wavelength, an effect called dispersion. Over long distances, the waves tend to sort themselves out, with the longest waves in the front and shorter ones in the rear.
Though dispersion is an important phenomenon among wind waves, tsunamis have such long wavelengths that their dispersion is very small.
Summary Questions
Question 1
Which of the following are data used by tsunami warning centers to forecast tsunami danger to coasts around an ocean basin? (Choose all that apply.)
The answers are A, B, C, E, F, and G. Meteorological data is not generally used because tsunami wave travel in deep ocean is generally unaffected by weather.
Question 2
Tsunamis generated by earthquakes with long rupture zones tend to "beam" less of their energy in one direction. (Choose the best answer.)
The correct answer is False.
Tsunamis generated by earthquakes with long rupture zones tend to "beam" more of their energy in one direction.
Question 3
(Use the selection box to choose the answer that best completes the statement.)
Tsunami waves reflect when they encounter obstructions.
Question 4
How does refraction affect waves? (Choose the best answer.)
The correct answer is A. Shallow water slows waves, causing refraction. Waves entering deeper water would experience less refraction, not more. Obstructing land would reflect waves, and the curvature of the earth does not affect refraction one way or the other.
Question 5
(Use the selection box to choose the answer that best completes the statement.)
Convergence causes waves to gain height after they travel more than one-quarter of the distance around the globe.
Question 6
(Use the selection box to choose the answer that best completes the statement.)
The answer is largest in front and smallest in back, because higher wavelength waves travel faster.